Considering fractions as proportional relationships between two numbers, a differentiation is established between those that exceed unity, called improper fractions, and those that do not, which are their own. For instance: 4/3, 21/11, 50/18.
Characteristics of improper fractions
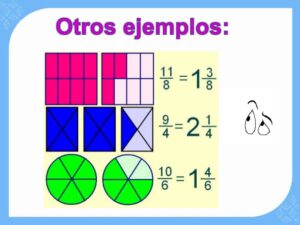
In improper fractions the numerator (the number that is at the top of the fraction) is always greater than its denominator (the one at the bottom), so it can also be expressed as the combination of a whole number and another fraction and less than 1.
There is talk of ‘combination‘, because in writing they appear that way: the whole number and to its right the fractional number. Although formally a ‘+’ sign should be written between the two, this is usually not done.
These numbers made up of a whole and a fraction are called mixed numbers, and they are often seen on signs of shops that sell products by weight.
For example, in an ice cream parlor, hardly someone chooses to order 5/2 of a kilo of ice cream (and much less in a higher ratio, such as 25/10), but he will surely request 2 ½, that is, “two and a half kilos” of ice cream.
The exercise of transform an improper fraction into a mixed number It’s simple: you have to decompose the numerator in such a way that it is divisible by the denominator, resulting in a whole number (in the example, 4/2 = 2), the remaining fraction (in this case ½) will be the fraction.
For the purposes of mathematical analysis, it is useless to express an improper fraction such as the number of units it has and the lesser quotient of one, since what matters is each number separately: the operations between fractions, as well as those that combine fractions and whole numbers are much simpler as you work with improper fractions.
Although the operations between proper and improper fractions are performed in the same way, there are certain differential characteristics in both cases, such as the fact that a multiplication between improper fractions results in an improper fraction.
While the division between improper fractions depends precisely on which number is placed as a dividend (numerator) and which as a divisor (denominator): if the first is greater than the second, then it will be an improper fraction, while if the second is the largest will be a proper fraction.
A particular case of improper fractions are those that result in a division in which there is no remainder, that is, one in which the numerator is a multiple of the denominator and then it is a whole number: these are known as apparent fractions.
Examples of improper fractions
Here are a number of examples of improper fractions:
- 4/3
- 11/21
- 50/18
- 100/17
- 10/9
- 8/23
- 33/4
- 9/21
- 72/33
- 41/8
- 11/10
- 3/2
- 7/17
- 6/5
- 41/5
- 100/99
- 414/200
- 121/100
- 77/10
- 32/9
