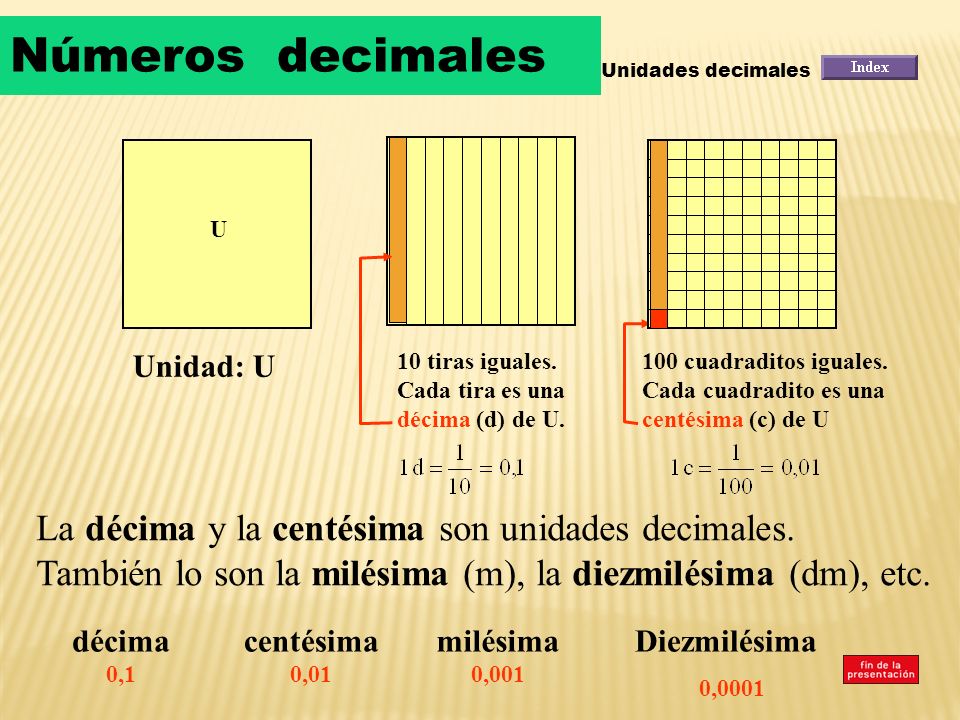
In the field of math, is recognized as decimal numbers to those that have an integer part, plus a decimal part other than 0. That is, they do not manage to compose an integer. For instance: 3 (3/10), 9 (19/10), 1 (1001/10).
 Decimal numbers are more difficult to imagine and represent mentally, and in general the only resource that is accepted to get a notion of what they are in fact is to size them as fractions, that is, as whole units divided. However, it can be seen by extension that not all decimal numbers are capable of being expressed as a fraction.
Decimal numbers are more difficult to imagine and represent mentally, and in general the only resource that is accepted to get a notion of what they are in fact is to size them as fractions, that is, as whole units divided. However, it can be seen by extension that not all decimal numbers are capable of being expressed as a fraction.
Decimal numbers make up one of the largest groups in the field of number distributions, practically the totality excluding the integers and the divisions that can only be made between them: the decimals will never be even or odd.
Within this group, for example, appear the:
- Exact decimal numbers. Those that have a finite number of decimal places.
- Recurring decimal numbers. Those that have an infinite quantity, as they come out of a division that results in an infinite decimal number, such as 1/3.

In another sense, the division appears between rational decimals (those that can be expressed as a fraction) and the irrational (Those that cannot be expressed like this, and have infinite non-periodic figures, such as the famous number pi or the square root of 2).
Decimal number expression
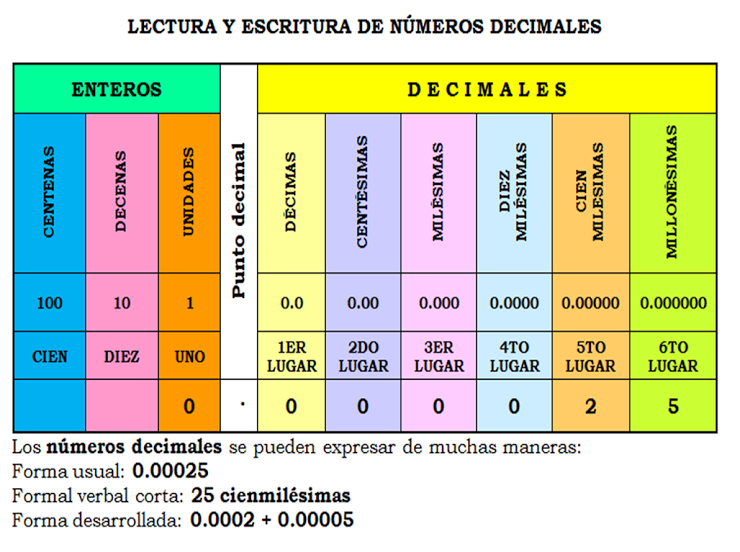
The way of express decimal numbersIn the event that you want to show the number and not the fraction, it is to place the integer to the left, and after a period the decimal numbers in an orderly way as if it were a new number.
This has a peculiarity, since unlike integers where the neutrality of 0 is to the left, in decimals the neutrality of 0 to the right is assumed: 0.4 is equal to 0.40 and 0.400, and of course greater than 0.39 and 0.399.
If you wanted to clarify the periodicity of a number, a sign should be placed above it or the numbers that want to be shown as periodic, these may not be the end of the decimal places.
List of examples of decimal numbers
The following list includes twenty examples of decimal numbers, accompanied by the irreducible fraction that represents them if they have one.
- 3 (3/10)
- 9 (10/19)
- 1 (1001/10)
- Π (pi number), 3.1415926535…. (not expressible as a fraction)
- 8 (14/5)
- 33 (33/100)
- 75 (883/4)
- 7 (37/10)
- 416666666666666666666 (to infinity) (101/12)
- 5 (3/2)
- 1 (71/100)
- Φ (golden number), (1 + 5 ^ (1/2)) / 2 (not expressible as a fraction itself, since the root of 5 is also irrational)
- 25 (217/4)
- 333333333333333 (to infinity) (4/3)
- 4 (22/50)
- 9 (59/100)
- 25 (5/4)
- 88888888888888 (to infinity) (71/9)
- 25 (4/13)
- 2 ^ (1/2) (cannot be expressed as a fraction)
