One of the typical categories of numerical analysis is that of the group of Prime numbers, defined as that integrated by the numbers that are only divisible by themselves (resulting in 1) and by 1 (resulting in themselves). For instance: 2, 17, 41, 53.
When you talk about ‘be divisible‘ It is referring to the fact that the result has to be a whole number, because strictly speaking, all numbers are divisible by all numbers (except for 0), yielding integer or fractional results.
From the above, some important conclusions can be drawn:
- Pair numbers. They cannot be prime, since all even numbers are divisible, in addition to two, by a certain number that results in two. An exception to this is the number two itself., which is prime by fulfilling the essential condition of being only divisible by itself and by the unit.
- Odd numbers. On the other hand, they can be prime, insofar as they cannot be expressed as the product of two other numbers.
Examples of prime numbers
The first twenty prime numbers are listed below as an example (note that number 1 is not included in this list, as it does not meet the prime number condition).
| 2 | 31 |
| 3 | 37 |
| 5 | 41 |
| 7 | 43 |
| 11 | 47 |
| 13 | 53 |
| 17 | 59 |
| 19 | 61 |
| 2. 3 | 67 |
| 29 | 71 |
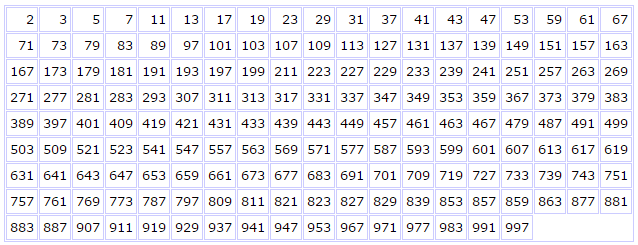
Table of prime numbers less than 1000
Prime Number Applications
Prime numbers are of great importance in the field of applications of the math, especially in matters of computing and security of virtual communications.
It happens that all the encryption system It is built on the basis of prime numbers, since the primality condition makes it impossible to decompose these numbers; which means that it is much more difficult to decipher the combination of digits under which a password is hidden.
Distribution of prime numbers
Working with prime numbers has a particular feature that is rare in mathematics, which makes it exciting for many mathematical experts: the fact that most of the theoretical elaborations they do not exceed the category of conjecture.
Although it has been shown that the prime numbers they are infinite, there is no concrete proof of their distribution among integers: the general statement of the prime number theorem states that the larger the numbers, the lower the chance of encountering a prime, but there are no theoretical elaborations that specifically explain what this distribution is like, in order to be able to identify all the prime numbers.
The combination between functionality of prime numbers and riddles Around them makes their analysis of great interest for mathematics, and that computers are programmed to find ever larger prime numbers. At the moment, the largest known prime number has more than 17 million digits, a figure that can only be calculated by means of computers that respond to very complex algorithms.
