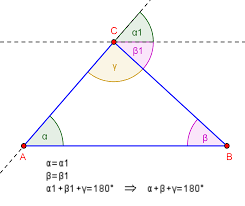
The meeting between two lines or rays always gives rise to the formation of a angle. In general, we speak of angles to refer to plane trigonometry, that is, the one that corresponds to the meeting between rays that do not have a curved shape but are a line. For instance: watered angle, obtuse angle, right angle.
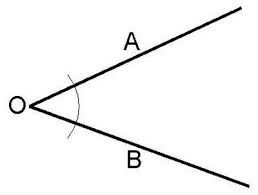
The point where the two rays touch is called vertex, and that is where the angle begins: it is an entity that does not have a physical delimitation but is there, starting from the vertex and until the two rays end or change shape.
It is common to seek to establish relationships of similarity or difference between the angles. When two angles have a vertex and a side in common, they are called in a row, while when they have the vertex in common but the sides continue in an opposite way (that is, the vertex is common but the angle is formed on the other side) they are called opposites by the vertex: the angles opposed by the vertex always have the same amplitude, and then they give rise to two pairs of angles of equal amplitude.
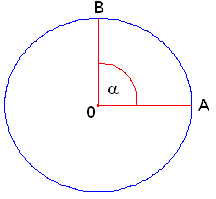
This happens because the angle cannot have an infinite amplitude but at most it will be that of the complete turn, 360 ° (degrees), 400 g (grads) or 2π radians. The angles that combine giving the entire turn are called supplementary, while those that do so generating a quarter of a turn are called complementary.
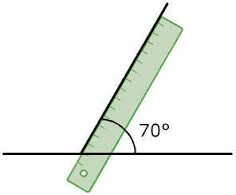
The question of the amplitudes of the angles is the mathematical foundation of trigonometry, and it was always indispensable in the matter of the mathematical applications of reality: everything that has to do with architectural and engineering constructions uses this type of procedure. The elementary tool for measuring the amplitude of an angle is the conveyor, which does not understand the entire turn but only half of it.
The measurement you use is that of degrees, so the maximum that you can capture is 180 °. The way to use the tool is to place the straight side of the protractor on one side of the angle, and check the angle value of the other side according to the scale of the protractor. That will be the angle, regardless of the length of the sides. According to the width of the sides, the most common classification of the angle measurement appears.
Examples of acute, obtuse, straight, and straight angles
- Acute angles. They are those with an amplitude less than 90 °, that is to say, a quarter turn. Equilateral triangles (those that have all their sides equal) are always composed of three 60 ° angles, that is, three acute angles.





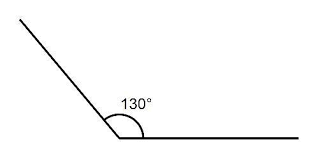
- Obtuse angles. They are those with an amplitude greater than 90 °, but less than 180 °. If any of the two rays extends beyond the vertex, it will be accompanied by a sharp one and will give rise to 180 °. If the two rays are longer than the vertex, there will be two pairs of opposite angles through the vertex to add up to 360 °.





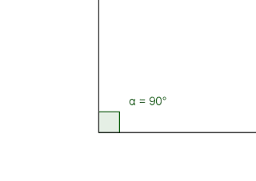
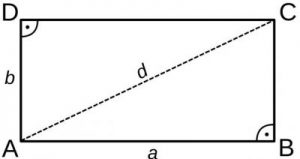
- Right angles. They are the ones that measure exactly 90 °. The symbology that is usually used to express this is the angle in the shape of a square instead of a circle. All squares and rectangles have four such angles, so inside they add up to 360 °.





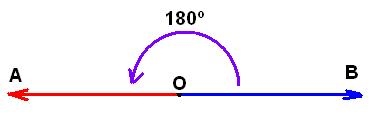
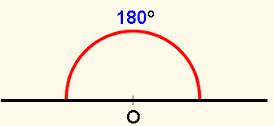
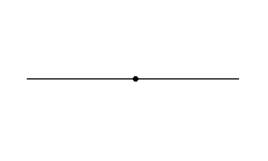
- Flat angles. They are the ones that have an amplitude of 180 °, so they represent half the turn. This means that, at first glance, the sides form a single ray that continues: any line, if you think about it this way, is made up of infinite vertices of 180 ° angles. A good example of the straight angle is the one generated by the hands of the clock when the time is 6:00.