15 Examples of Elliptical Motion

It is understood by elliptical motion which describes a path in the form of an ellipse, that is, a circle flattened at two of its ends, like the one that appears at the base of a cone. The ellipse is characterized by having two foci for which the sum of the distances to any point of the ellipse is constant.

Elliptical motion occurs in nature due to the presence of central force fields, such as the harmonic potential field and the Newtonian gravitational potential, each with a specific theoretical and mathematical formulation.

For the first case the potential is written as:

V (x, y) = k / 2 (x^two+ and^two),

Where K is a constant that depends on the harmonic oscillator and for the second:

V (x, y, z) = – (GM) / (√ (x^two+ and^two+ z^two))

Where M is a mass that generates a gravitational field and G is the universal constant of gravity. In both cases x, y, z, are spatial coordinates in three dimensions.

This type of movement is very common in everyday life. Even circular motion is nothing more than a special shape of the elliptical.

Examples of elliptical motion

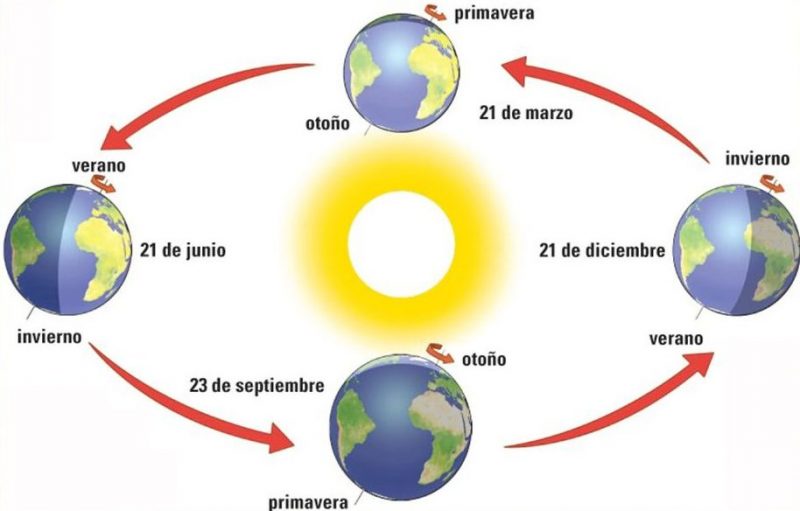
1. Orbital translation. Planets, asteroids, comets, natural satellites move along an orbit and do so in an elliptical way, attracted by the gravity of some star or object of greater mass, such as the earth around the Sun and the Moon around is.
2. Parabolic shot. When a projectile is launched, it describes a parabolic trajectory since the speed in the horizontal direction is constant and in the vertical axis, due to gravity, it changes. If the angle with respect to the horizontal with which the projectile is thrown is varied, and the initial launch velocity is kept fixed, it can be seen that the highest point of the parabola describes an ellipse.
3. The turn of an elliptical bike. Bicycles called elliptical trainers are machines used for exercising. The legs rotate the pedals that, when traveling a complete path, describe an ellipse.
4. The hula hoop (or hula hoop). It is a game that requires a ring that is rotated with some part of the body, most commonly the waist. During the turn, an elliptical path is described.
5. A type of pendulum swing. If you have a pendulum at rest, you remove it from the equilibrium position and instead of releasing it and letting it oscillate, you give it an impulse in some direction other than that from which it was removed, the pendulum will describe an elliptical path.
6. The movement of the swing. These static and suspended toys trace a perfectly discernible elliptical path in their swing, although analyzable (as in the case of projectiles) from parabolic laws.
7. An egg spinning on its axis. Although unusual, this example is appropriate, as the egg is not circular, but oval, and as it rotates on its axis it traces a perfect ellipse.
8. The axis of a top or spinning top. Although in its initial moments it remains straighter, as it loses strength in its turn, the axis of this toy tilts and traces less and less circular shapes, close to the ellipse.
9. The path of the electrons. According to the classical (and non-quantum) description, oscillating around the nucleus of an atom are electrons, negatively charged particles attracted by the protons of the nucleus along their elliptical paths.
10. The twist of the rope of a Cowboy. The path traced by the lasso with which the cowboys of yesteryear tied horses and cattle is elliptical above their heads.
11. The path of a boomerang. In their passage through the air, these striking tools trace a perfect ellipse, in one of whose foci the launcher would be located.
12. Artificial satellites. Floating in the outer margin of the Earth’s atmosphere, artificial satellites for communications and scientific affairs behave like any celestial object, tracing an elliptical orbit around the earth.
13. An object hanging from a spring. When released, the mass hanging from a spring (like a man jumping into bungee, for example) will descend and rise again, tracing an ellipse around two different foci: an upper position and a lower position.