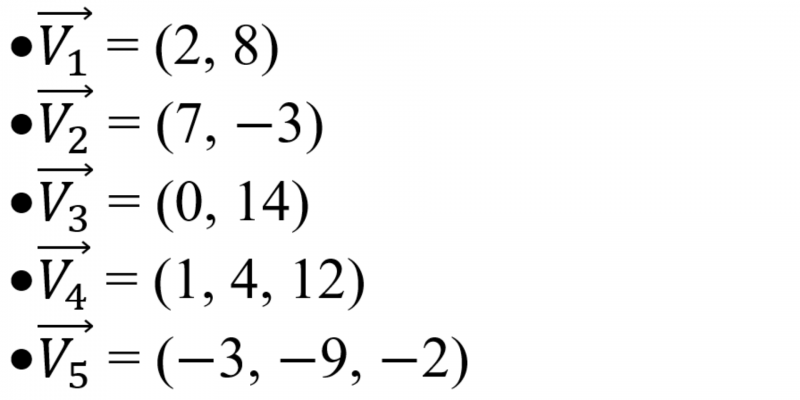A vector is a mathematical tool, generally used in geometry and physics, that allows to carry out calculations and operations.
In physics, a vector is a line segment in space that has modulus (also called length) and direction (or orientation). Vectors are graphed with an arrow and help describe vector quantities.
Vector quantities are represented through a vector because they cannot be determined by a single real number, but it is necessary to know its direction and sense. For example: speed, displacement. This distinguishes them from scalar quantities, which only require a number and a certain unit of measure to be defined, for example: pressure, volume, temperature.
In mathematics, vectors are the elements of a vector space. This notion is more abstract, since in many vector spaces the vector cannot be defined from module and direction, for example: vectors in infinite-dimensional spaces. The representation used to represent a vector in a space of “n” dimensions is: v= (a1, a2, a3,… an)
Vectors can be added or subtracted from each other to give rise to a new resultant vector, or multiplied by a scalar, vector, or mixed value.
Elements of a vector
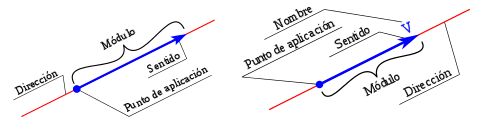
To fully define a vector, you must specify three characteristics that distinguish one vector from another:
- Module. It is determined by the length or length of the line segment.
- Direction. It is determined by the orientation of the line in the plane.
- Sense. It is determined by the origin and endpoint of the line segment.
Types of vectors
Different classes of vectors can be distinguished according to the characteristics they present and the relationship they have with other vectors:
- Unit vectors. Vectors whose modulus is equal to 1.
- Free Vectors. Vectors that are not applied at any particular point.
- Vectors sliders. Vectors whose point of application slides along the line of action.
- Fixed vectors (or linked vectors). Vectors that are applied to a particular point.
- Collinear vectors. Two or more vectors that act on the same action line.
- Concurrent vectors (or angular vectors). Two or more vectors whose directions pass through the same point, forming an angle when the rays intersect.
- Parallel Vectors. Two or more vectors acting on a rigid body with parallel lines of action.
- Opposite Vectors. Vectors that have the same direction and the same module, but that have opposite directions.
- Vectors coplanar. Vectors whose lines of action lie in the same plane.
- Resulting vectors. Given a system of vectors, it is the vector that produces the same effect as all the component vectors of the system.
- Vectors balancing. Vector with the same magnitude and direction as the resulting vector, but with the opposite sense.
Vectors in everyday life
Vectors are widely used in many areas of everyday life because they allow us to know magnitudes and represent them based on their module, meaning and direction.
They are usually used to:
- Mark tours. All the routes that an individual makes, both on foot and in some form of transport, involve one or more vectors. These vectors are the ones that give meaning to the route because they delimit distances and direction. This function is widely used by GPS to mark paths or routes from one point of the plane to another.
- Measure distances. Vectors allow us to measure the distance from one point to another and calculate how long it will take to make the journey according to the speed, the means of transport, among other variables
- Practice sports. Vectors are the magnitudes that intervene during the practice of many games and sports, since they determine the direction and the sense that the individual will give to an element, such as a ball. Vectors allow you to calculate distances and make shots to other players or make a basket. The importance of vectors in this area can be seen very clearly in sports such as billiards, in which the player uses part of a segment to guide the course of the ball.
- Playing video games. Vectors are widely used when positioning and measuring elements within a space. This allows the player in video games to move and direct objects or characters from one point of the plane to another.
- Perform air traffic control. Vectors are used in the air environment to give a direction and sense to the aircraft and so that the pilots can direct it from one point to another.
- Driving a means of transport. Vectors are essential to draw and delimit orientations and directions, so they are used in transport so that the driver knows the route and the route.
- Calculate forces and accelerations. Vectors allow us to calculate the velocity of moving objects and also their accelerations. In addition, they are used to obtain other types of measurements, such as the sides of a building.
- Design roads and highways. Vectors are used in the field of architecture, design and construction to carry out buildings and constructions such as buildings, roads and bridges.
- Move objects. Knowing the distances and the meaning of the vectors allows the individual to manipulate elements (and his own person) to achieve certain ends. This is what allows a person to put a cup of tea in his mouth or to direct the umbrella according to the direction of the rain.
Vectors in two and three dimensions
Vectors can be represented in two-dimensional (“x”, “y”) or three-dimensional (“x”, “y”, “z”) spaces. In any case, the vectors can be defined by their coordinates in each of the axes.
In the case of a two-dimensional space, any vector can be defined as: v = (vx, vY). The terms in parentheses are the coordinates on the “x” and “y” axes.
On the other hand, in a three-dimensional space, a vector is defined as: v = (vx, vY, vz). One more coordinate is added to indicate the coordinate on the “z” axis.
Graphic representation of vectors
Vectors are generally represented using a two- or three-dimensional plane.
- First, the support or direction line is graphed, on which several vectors can exist, drawing a line segment that arises from the origin.
- Second, the length of the vector is marked, which is determined by the module (the greater the module, the longer the ray), and which is directed to a direction or point of application (which is why the vectors are drawn as arrows pointing in the direction in question).
- Finally, the name of the vector is written on the application point.
Examples of vector quantities in physics
- Density
- Speed
- Displacement
- Normal strength
- Acceleration
- electric field
- Magnetic field
- Gravitational field
- Weight
- Angular velocity
- Angular acceleration
- Frictional force
Examples of vectors in mathematics